Linear Sieve

1. 에라토스테네스의 체와 선형 체

고대 그리스 수학자인 에라토스테네스가 고안한 에라토스테네스의 체를 이용하면 1부터 N까지의 소수를 쉽게 뽑아 낼 수 있다.

n이하의 수에서 모든 소수를 찾고 싶다면 다음과 같은 알고리즘으로 찾을 수 있다.

2부터 N까지 수를 나열한다.
먼저 p를 소수인 2로 설정한다.
다음 2p부터 n까지 p의 배수를 제거한다.
남은 수 중 가장 작은 수를 p로 설정한다. 해당 수가 없다면 끝냅니다. 있다면 3번부터 다시 반복한다.
완료되었다면 n이하의 수에서 모든 소수가 남아있습니다.

예를 들어 20이하의 수에서 모든 소수를 찾고자 하려면, 먼저 20까지 나열한다.

2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

다음 2를 남기고 2의 배수를 제거한다.

2 3 5 7 9 11 13 15 17 19

다음 수인 3을 남기고 3의 배수를 제거한다.

2 3 5 7 11 13 17 19

이를 5, 7, 11, 13, 17, 19에 대해 반복하면 남는 수는 다음과 같다.

2 3 5 7 11 13 17 19

해당 과정을 C++코드로 작성하면 다음과 같이 작성할 수 있다.

std::vector<int> prime;
bool is_composite[MAX_N];

void sieve(int n){
    std::fill(is_composite, is_composite+n, false); 
    for(int i=2;i<n;i++){ 
        if(!is_composite[i]) prime.push_back(i); 
        // 2p부터 n까지 제거한다. 
        for(int j=i+1;i*j<n;j++){  
            is_composite[i*j]=true;
        }
    }
}

하지만 해당 코드의 공간복잡도 $O(n)$이고, 시간복잡도는 $O(nlogn)$입니다. 합성수인지 확인하는 과정에서 계산이 여러번 이루어지고, 만약 합성수를 확인하는 과정에서 한번만 확인하도록 변경하면 시간이 더 줄어들 것이다.

std::vector<int> prime;
bool is_composite[MAX_N];

void optimized_sieve(int n){
    std::fill(is_composite, is_composite+n, false); 
    for(int i=2;i<n;i++){ 
        if(!is_composite[i]) prime.push_back(i); 
        
        for(int j=0;j<prime.size() && i*prime[j]<n;j++){  
            is_composite[i*prime[j]]=true;
            if(i%prime[j] == 0) break;
        }
    }
}

위 코드는 합성수 q를 q=i*p로 표현가능하다는 아이디어에서 착안되었다. (여기서 p는 최소 소인수) p보다 적은 소수는 i를 나눌 수 없다는 사실에서 만약 i % prime[j] == 0인 경우면 p는 i의 소인수란 뜻이고 이미 그전의 합성수들은 처리되었다는 뜻이다.

2. 성능 비교

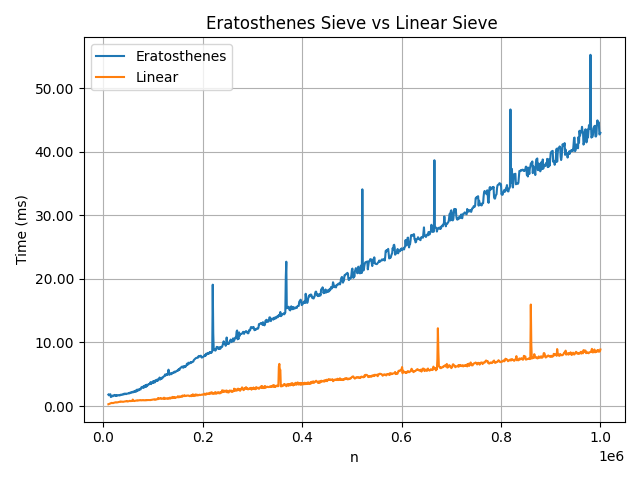
n을 10000부터 1000000까지 증가하며 두 코드를 비교한 그래프이다. 평균적으로 에라토스테네스의 체보다 선형 체가 빠른 것을 확인 할 수 있습니다. 또 시간복잡도 상수또한 선형 체가 더 낮은 것 또한 볼 수 있다.

1. 에라토스테네스의 체와 선형 체

2. 성능 비교

References